
In case the diameter d is known and the radius is not known to us, we can rewrite the radius as half of the diameter: Then, we can describe the diameter of a semi-circle as twice the length of its radius:Ĭombining these expressions, we can now express the perimeter as a sum in terms of the radius r:įinally, grouping the terms we arrive at the formula for the perimeter of a semi-circle: In other words, we can say that the length of the arc is half of the circumference of a circle: Next, we know that the length of the arc spans half of a circle. Perimeter=Length of Arc+Length of Diameter Hence, we can say that the perimeter of a semi-circle can be expressed as the sum of the length of the arc and the length of the diameter of the semi-circle: In a semi-circle, we have two edges: a curved arc and a diameter. We know that the perimeter can be defined as the sum of the lengths of all edges covering a shape. Derivation of the Perimeter Formula of a Semi-Circle We first derive the basic formula involved, provide intuitive insights, and then show how we apply this formula with some examples. This means that the exact decimal value of pi is a never-ending stream of numbers! However, for most cases we only round off the value of to the nearest hundredths:įrom the definitions provided earlier, we can now discuss in detail the formula for solving the perimeter of a semi-circle. It is important to note that this constant is a non-terminating irrational number. If we measure the perimeter of a circle and divide it with the measure of its diameter, we get the approximate value of pi: The mathematical constant pi, denoted by, is a number that relates the diameter of a circle to its circumference. What is Pi?īefore we proceed with computing for the perimeter and area of a semi-circle, we also introduce a special number that will prove relevant to our computations later.
In this sense, we can measure a shape’s area through the shape’s dimensions. Each object takes up some space in the room, depending on the kind of object and its size. Intuitively, we can think of shapes in a plane as objects in a room. On the other hand, we can define the area of a two-dimensional shape as a measure of the space it occupies in the two-dimensional plane.

Thus, for any closed shape we can get its perimeter by taking the length of the edges enclosing the shape. If we begin measuring the distance from the start of the lap, and then trace a closed path until we get back to the starting point, we can measure the perimeter of the park through the lap we have ran across: In an intuitive approach, we can relate the idea of a perimeter to how far we jog through a lap in the park. We define the perimeter of a two-dimensional shape as a measure of the boundary enclosing it. A line connecting the center to any point in the arc of the semicircle has a length equal to the radius of the semicircle. Like a circle, any point in the arc of the semicircle is equidistant from its center. To visualize, here is what a semi-circle looks like: We can think of a circle being sliced into two halves, and both shapes turn out to be semi-circles. What is a Semi-Circle?Ī semi-circle, by definition, is half of a circle. While doing so, we will also try some examples to guide us in learning. In this article, we learn the fundamental concepts starting with definitions of the shape, then we quantify the properties of the semi-circle by defining both its perimeter and then its area. From a taco inside the restaurant to the moon during a half-moon, we observe these things to have a semi-circular shape. What is the Area Formula of a Semi-Circle?Īs we explore more geometry concepts, we encounter another two-dimensional shape called a semi-circle.Derivation of the Area Formula of a Semi-Circle.What is the Perimeter Formula of a Semi-Circle?.Derivation of the Perimeter Formula of a Semi-Circle.This is the total length of the edge around the circle with the specified diameter, if it was straightened out.
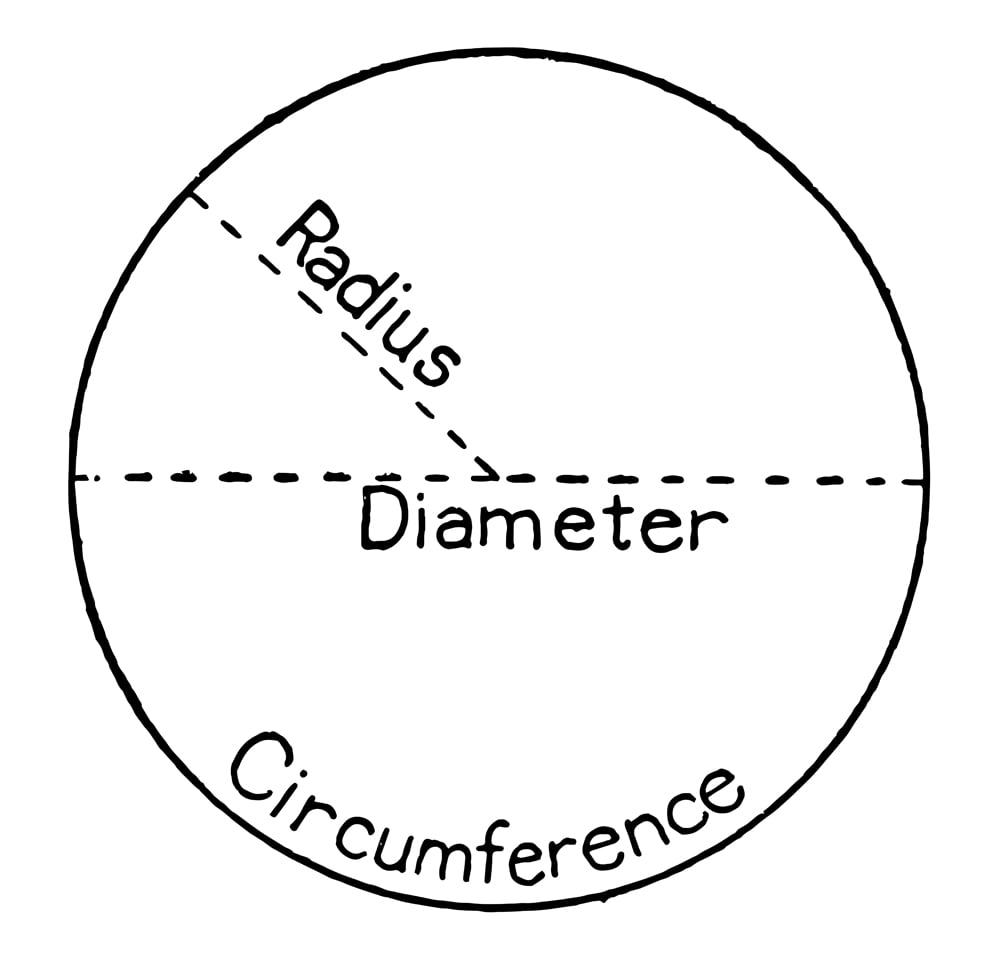
The diameter of a circle is the length of a straight line drawn between two points on a circle where the line also passes through the centre of a circle, or any two points on the circle as long as they are exactly 180 degrees apart. The formula used to calculate circle circumference is:Įnter the diameter of a circle. This tool will calculate the circumference of a circle from the diameter, and will convert different measurement units for diameter and circumference.


 0 kommentar(er)
0 kommentar(er)
